搜索到
84
篇与
的结果
-
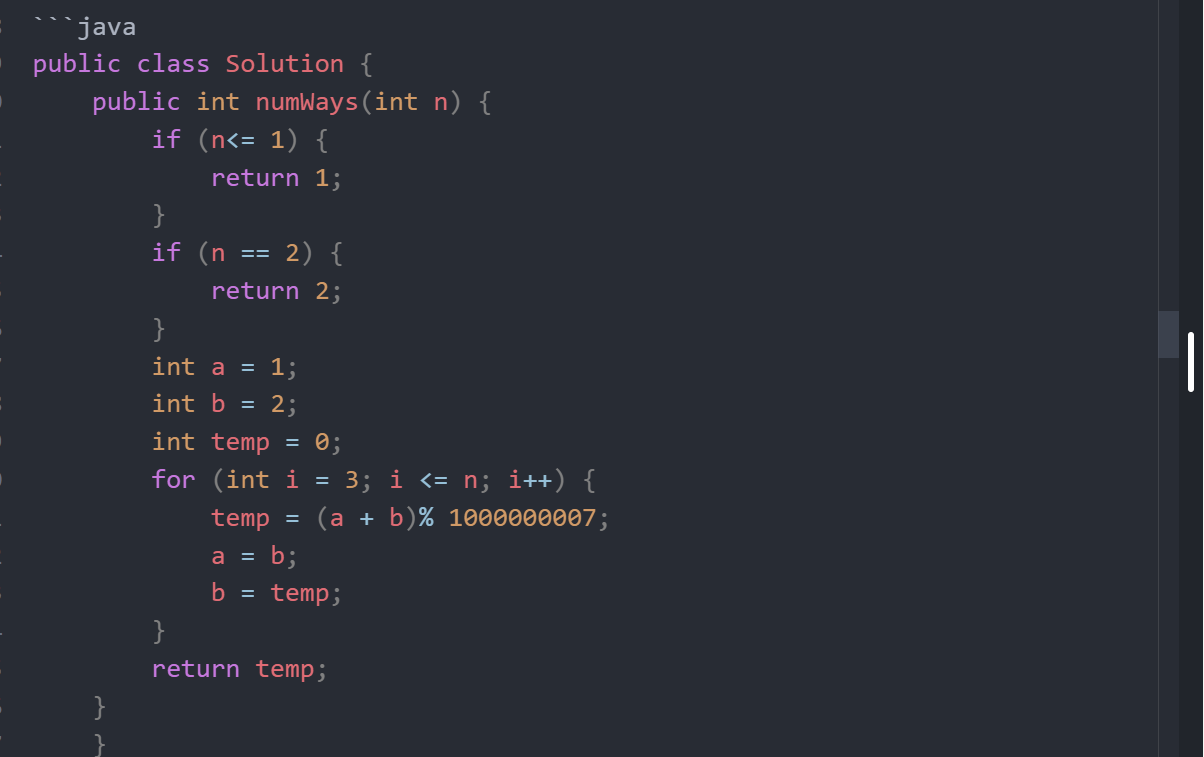
每日一个算法思想 - 动态规划（DP） 今天了解的算法思想的动态规划，这个内容算是算法里面比较重要的内容了。动态规划的英文名字叫做 Dynamic programming 这个不重要 直接学习思想简单来说就是拆分子问题，记住过往，减少重复计算量,接下来我将会举一个例子，让你快速理解说明是动态规划的含义。A ： "1+1+1+1+1+1+1+1 =？"A ： "上面等式的值是多少"B ： 计算 "8"A : 在上面等式的左边写上 "1+" 呢？A : "此时等式的值为多少"B : 很快得出答案 "9"A : "你怎么这么快就知道答案了"A : "只要在8的基础上加1就行了"A : "所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"上面就是一个简单的例子说明所以说上面看明白了吗一个例子带你走进动态规划 -- 青蛙跳阶问题暴力递归★ leetcode原题：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。”有些小伙伴第一次见这个题的时候，可能会有点蒙圈，不知道怎么解决。其实可以试想：★要想跳到第10级台阶，要么是先跳到第9级，然后再跳1级台阶上去;要么是先跳到第8级，然后一次迈2级台阶上去。同理，要想跳到第9级台阶，要么是先跳到第8级，然后再跳1级台阶上去;要么是先跳到第7级，然后一次迈2级台阶上去。要想跳到第8级台阶，要么是先跳到第7级，然后再跳1级台阶上去;要么是先跳到第6级，然后一次迈2级台阶上去。”假设跳到第n级台阶的跳数我们定义为f(n)，很显然就可以得出以下公式：f（10） = f（9）+f(8)f (9) = f(8) + f(7)f (8) = f(7) + f(6)...f(3) = f(2) + f(1)即通用公式为: f(n) = f(n-1) + f(n-2)那f(2) 或者 f(1) 等于多少呢？当只有2级台阶时，有两种跳法，第一种是直接跳两级，第二种是先跳一级，然后再跳一级。即f(2) = 2;当只有1级台阶时，只有一种跳法，即f（1）= 1；因此可以用递归去解决这个问题：class Solution {public int numWays(int n) { if(n == 1){ return 1; } if(n == 2){ return 2; } return numWays(n-1) + numWays(n-2); }}去leetcode提交一下，发现有问题，超出时间限制了为什么超时了呢？递归耗时在哪里呢？先画出递归树看看：要计算原问题 f(10)，就需要先计算出子问题 f(9) 和 f(8)然后要计算 f(9)，又要先算出子问题 f(8) 和 f(7)，以此类推。一直到 f(2) 和 f(1），递归树才终止。我们先来看看这个递归的时间复杂度吧：递归时间复杂度 = 解决一个子问题时间*子问题个数一个子问题时间 = f（n-1）+f（n-2），也就是一个加法的操作，所以复杂度是 O(1)；问题个数 = 递归树节点的总数，递归树的总节点 = 2^n-1，所以是复杂度O(2^n)。因此，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n)，就是指数级别的，爆炸增长的，如果n比较大的话，超时很正常的了。回过头来，你仔细观察这颗递归树，你会发现存在大量重复计算，比如f（8）被计算了两次，f（7）被重复计算了3次...所以这个递归算法低效的原因，就是存在大量的重复计算！既然存在大量重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去备忘录查一下，如果有，就直接取就好了，备忘录没有才开始计算，那就可以省去重新重复计算的耗时啦！这就是带备忘录的解法。带备忘录的递归解法（自顶向下）一般使用一个数组或者一个哈希map充当这个备忘录。第一步，f（10）= f(9) + f(8)，f(9) 和f（8）都需要计算出来，然后再加到备忘录中，如下：第二步， f(9) = f（8）+ f（7），f（8）= f（7）+ f(6), 因为 f(8) 已经在备忘录中啦，所以可以省掉，f(7),f（6）都需要计算出来，加到备忘录中~第三步， f(8) = f（7）+ f(6),发现f(8)，f(7),f（6）全部都在备忘录上了，所以都可以剪掉。所以呢，用了备忘录递归算法，递归树变成光秃秃的树干咯，如下：带备忘录的递归算法，子问题个数=树节点数=n，解决一个子问题还是O(1),所以带备忘录的递归算法的时间复杂度是O(n)。接下来呢，我们用带备忘录的递归算法去撸代码，解决这个青蛙跳阶问题的超时问题咯~，代码如下：public class Solution { //使用哈希map，充当备忘录的作用 Map<Integer, Integer> tempMap = new HashMap(); public int numWays(int n) { // n = 0 也算1种 if (n == 0) { return 1; } if (n <= 2) { return n; } //先判断有没计算过，即看看备忘录有没有 if (tempMap.containsKey(n)) { //备忘录有，即计算过，直接返回 return tempMap.get(n); } else { // 备忘录没有，即没有计算过，执行递归计算,并且把结果保存到备忘录map中，对1000000007取余（这个是leetcode题目规定的） tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007); return tempMap.get(n); } } }去leetcode提交一下，如图，稳了：其实，还可以用动态规划解决这道题。自底向上的动态规划动态规划跟带备忘录的递归解法基本思想是一致的，都是减少重复计算，时间复杂度也都是差不多。但是呢：带备忘录的递归，是从f(10)往f(1）方向延伸求解的，所以也称为自顶向下的解法。动态规划从较小问题的解，由交叠性质，逐步决策出较大问题的解，它是从f(1)往f(10）方向，往上推求解，所以称为自底向上的解法。动态规划有几个典型特征，最优子结构、状态转移方程、边界、重叠子问题。在青蛙跳阶问题中：f(n-1)和f(n-2) 称为 f(n) 的最优子结构f(n)= f（n-1）+f（n-2）就称为状态转移方程f(1) = 1, f(2) = 2 就是边界啦比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。我们来看下自底向上的解法，从f(1)往f(10）方向，想想是不是直接一个for循环就可以解决啦，如下：带备忘录的递归解法，空间复杂度是O(n)，但是呢，仔细观察上图，可以发现，f（n）只依赖前面两个数，所以只需要两个变量a和b来存储，就可以满足需求了，因此空间复杂度是O(1)就可以啦动态规划实现代码如下：public class Solution { public int numWays(int n) { if (n<= 1) { return 1; } if (n == 2) { return 2; } int a = 1; int b = 2; int temp = 0; for (int i = 3; i <= n; i++) { temp = (a + b)% 1000000007; a = b; b = temp; } return temp; } }动态规划的解题套路什么样的问题可以考虑使用动态规划解决呢？★ 如果一个问题，可以把所有可能的答案穷举出来，并且穷举出来后，发现存在重叠子问题，就可以考虑使用动态规划。”比如一些求最值的场景，如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等，都是动态规划的经典应用场景。动态规划的解题思路动态规划的核心思想就是拆分子问题，记住过往，减少重复计算。 并且动态规划一般都是自底向上的，因此到这里，基于青蛙跳阶问题，我总结了一下我做动态规划的思路：穷举分析确定边界找出规律，确定最优子结构写出状态转移方程穷举分析当台阶数是1的时候，有一种跳法，f（1） =1当只有2级台阶时，有两种跳法，第一种是直接跳两级，第二种是先跳一级，然后再跳一级。即f(2) = 2;当台阶是3级时，想跳到第3级台阶，要么是先跳到第2级，然后再跳1级台阶上去，要么是先跳到第 1级，然后一次迈 2 级台阶上去。所以f(3) = f(2) + f(1) =3当台阶是4级时，想跳到第3级台阶，要么是先跳到第3级，然后再跳1级台阶上去，要么是先跳到第 2级，然后一次迈 2 级台阶上去。所以f(4) = f(3) + f(2) =5当台阶是5级时......确定边界通过穷举分析，我们发现，当台阶数是1的时候或者2的时候，可以明确知道青蛙跳法。f（1） =1，f(2) = 2，当台阶n>=3时，已经呈现出规律f(3) = f(2) + f(1) =3，因此f（1） =1，f(2) = 2就是青蛙跳阶的边界。找规律，确定最优子结构n>=3时，已经呈现出规律 f(n) = f(n-1) + f(n-2) ，因此，f(n-1)和f(n-2) 称为 f(n) 的最优子结构。什么是最优子结构？有这么一个解释：★ 一道动态规划问题，其实就是一个递推问题。假设当前决策结果是f(n),则最优子结构就是要让 f(n-k) 最优,最优子结构性质就是能让转移到n的状态是最优的,并且与后面的决策没有关系,即让后面的决策安心地使用前面的局部最优解的一种性质”4， 写出状态转移方程通过前面3步，穷举分析，确定边界，最优子结构，我们就可以得出状态转移方程啦：代码实现我们实现代码的时候，一般注意从底往上遍历哈，然后关注下边界情况，空间复杂度，也就差不多啦。动态规划有个框架的，大家实现的时候，可以考虑适当参考一下：dp0[...] = 边界值for(状态1 ：所有状态1的值){for(状态2 ：所有状态2的值){ for(...){ //状态转移方程 dp[状态1][状态2][...] = 求最值 } }}leetcode案例分析我们一起来分析一道经典leetcode题目吧★ 给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。”示例 1：输入：nums = [10,9,2,5,3,7,101,18]输出：4解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。示例 2：输入：nums = [0,1,0,3,2,3]输出：4我们按照以上动态规划的解题思路，穷举分析确定边界找规律，确定最优子结构状态转移方程1.穷举分析因为动态规划，核心思想包括拆分子问题，记住过往，减少重复计算。 所以我们在思考原问题：数组num[i]的最长递增子序列长度时，可以思考下相关子问题，比如原问题是否跟子问题num[i-1]的最长递增子序列长度有关呢？自顶向上的穷举这里观察规律，显然是有关系的，我们还是遵循动态规划自底向上的原则，基于示例1的数据，从数组只有一个元素开始分析。当nums只有一个元素10时，最长递增子序列是[10],长度是1.当nums需要加入一个元素9时，最长递增子序列是[10]或者[9],长度是1。当nums再加入一个元素2时，最长递增子序列是[10]或者[9]或者[2],长度是1。当nums再加入一个元素5时，最长递增子序列是[2,5],长度是2。当nums再加入一个元素3时，最长递增子序列是[2,5]或者[2,3],长度是2。当nums再加入一个元素7时，,最长递增子序列是[2,5,7]或者[2,3,7],长度是3。当nums再加入一个元素101时，最长递增子序列是[2,5,7,101]或者[2,3,7,101],长度是4。当nums再加入一个元素18时，最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4。当nums再加入一个元素7时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4.分析找规律，拆分子问题通过上面分析，我们可以发现一个规律：如果新加入一个元素nums[i], 最长递增子序列要么是以nums[i]结尾的递增子序列，要么就是nums[i-1]的最长递增子序列。看到这个，是不是很开心，nums[i]的最长递增子序列已经跟子问题 nums[i-1]的最长递增子序列有关联了。原问题数组nums[i]的最长递增子序列 = 子问题数组nums[i-1]的最长递增子序列/nums[i]结尾的最长递增子序列是不是感觉成功了一半呢？但是如何把nums[i]结尾的递增子序列也转化为对应的子问题呢？要是nums[i]结尾的递增子序列也跟nums[i-1]的最长递增子序列有关就好了。又或者nums[i]结尾的最长递增子序列，跟前面子问题num[j]（0=<j<i）结尾的最长递增子序列有关就好了，带着这个想法，我们又回头看看穷举的过程：nums[i]的最长递增子序列，不就是从以数组num[i]每个元素结尾的最长子序列集合，取元素最多（也就是长度最长）那个嘛，所以原问题，我们转化成求出以数组nums每个元素结尾的最长子序列集合，再取最大值嘛。哈哈，想到这，我们就可以用dp[i]表示以num[i]这个数结尾的最长递增子序列的长度啦，然后再来看看其中的规律：其实，nums[i]结尾的自增子序列，只要找到比nums[i]小的子序列，加上nums[i] 就可以啦。显然，可能形成多种新的子序列，我们选最长那个，就是dp[i]的值啦★nums[3]=5,以5结尾的最长子序列就是[2,5],因为从数组下标0到3遍历，只找到了子序列[2]比5小，所以就是[2]+[5]啦，即dp[4]=2nums[4]=3,以3结尾的最长子序列就是[2,3],因为从数组下标0到4遍历，只找到了子序列[2]比3小，所以就是[2]+[3]啦，即dp[4]=2nums[5]=7，以7结尾的最长子序列就是[2,5,7]和[2,3,7],因为从数组下标0到5遍历，找到2,5和3都比7小，所以就有[2,7],[5,7],[3,7],[2,5,7]和[2,3,7]这些子序列，最长子序列就是[2,5,7]和[2,3,7]，它俩不就是以5结尾和3结尾的最长递增子序列+[7]来的嘛！所以，dp[5]=3 =dp[3]+1=dp[4]+1。”很显然有这个规律：一个以nums[i]结尾的数组nums如果存在j属于区间[0，i-1],并且num[i]>num[j]的话，则有，dp(i) =max(dp(j))+1，最简单的边界情况当nums数组只有一个元素时，最长递增子序列的长度dp(1)=1,当nums数组有两个元素时，dp(2) =2或者1， 因此边界就是dp(1)=1。确定最优子结构从穷举分析，我们可以得出，以下的最优结构：dp(i) =max(dp(j))+1，存在j属于区间[0，i-1],并且num[i]>num[j]。max(dp(j)) 就是最优子结构。状态转移方程通过前面分析，我们就可以得出状态转移方程啦：所以数组num[i]的最长递增子序列就是：最长递增子序列 =max(dp[i])代码实现class Solution { public int lengthOfLIS(int[] nums) { if (nums.length == 0) { return 0; } int[] dp = new int[nums.length]; //初始化就是边界情况 dp[0] = 1; int maxans = 1; //自底向上遍历 for (int i = 1; i < nums.length; i++) { dp[i] = 1; //从下标0到i遍历 for (int j = 0; j < i; j++) { //找到前面比nums[i]小的数nums[j],即有dp[i]= dp[j]+1 if (nums[j] < nums[i]) { //因为会有多个小于nums[i]的数，也就是会存在多种组合了嘛，我们就取最大放到dp[i] dp[i] = Math.max(dp[i], dp[j] + 1); } } //求出dp[i]后，dp最大那个就是nums的最长递增子序列啦 maxans = Math.max(maxans, dp[i]); } return maxans; } } -
-
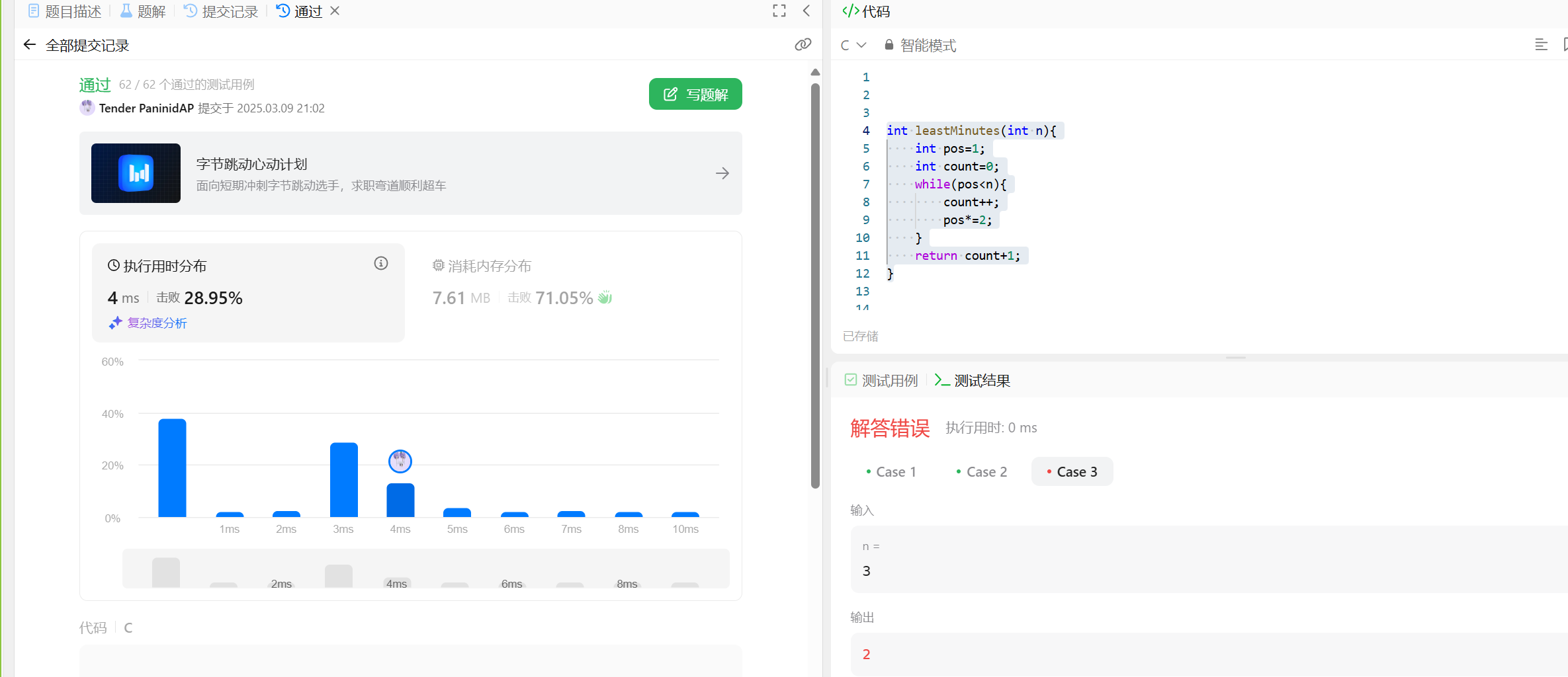
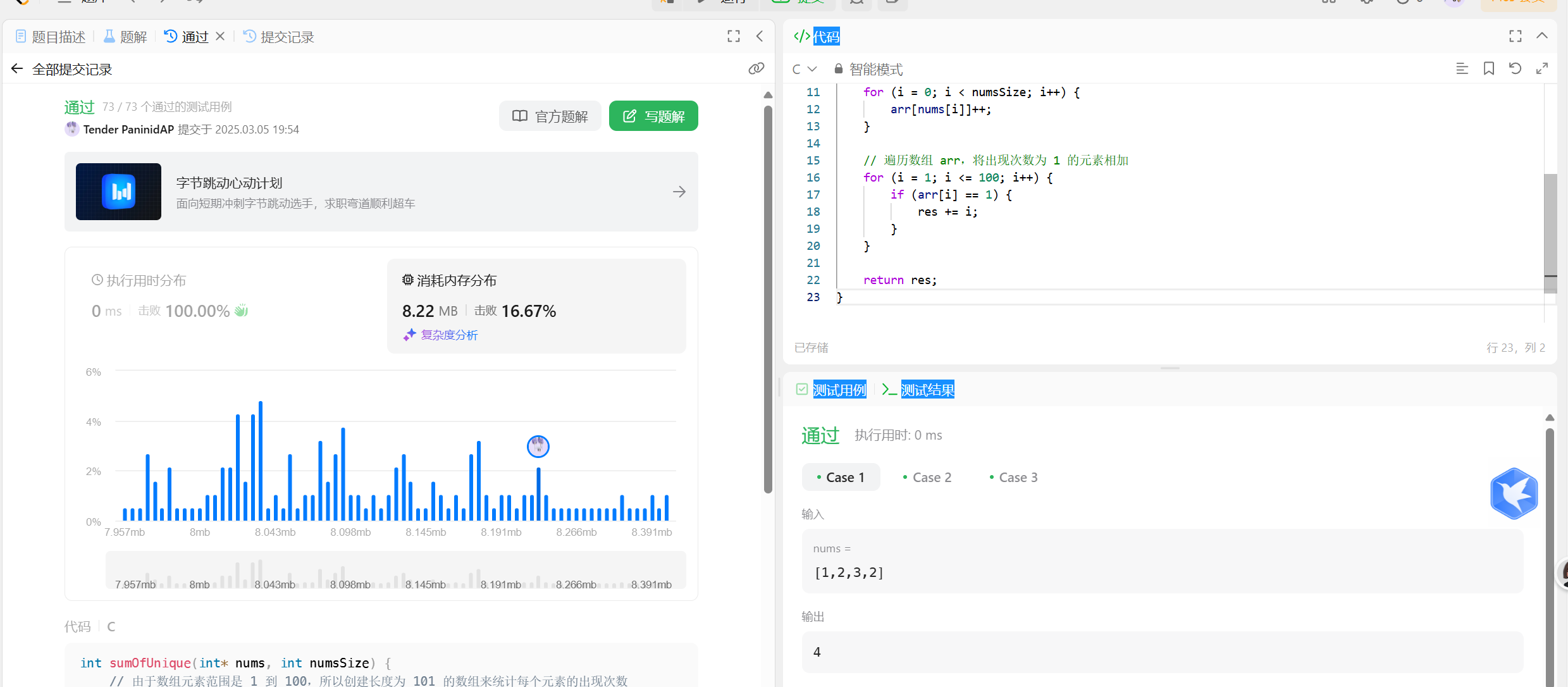
力扣1748唯一元素的和 还是比较简单的 直接哈希丝滑小连招上题目代码测试用例测试用例测试结果唯一元素的和已解答简单相关标签相关企业提示给你一个整数数组 nums 。数组中唯一元素是那些只出现 恰好一次 的元素。请你返回 nums 中唯一元素的 和 。示例 1：输入：nums = [1,2,3,2]输出：4解释：唯一元素为 [1,3] ，和为 4 。示例 2：输入：nums = [1,1,1,1,1]输出：0解释：没有唯一元素，和为 0 。示例 3 ：输入：nums = [1,2,3,4,5]输出：15解释：唯一元素为 [1,2,3,4,5] ，和为 15 。提示：1 <= nums.length <= 1001 <= nums[i] <= 100那么代码也很简单int sumOfUnique(int* nums, int numsSize) { int arr[102]; int res = 0; int i =0; memset(arr,0,sizeof(int) * 102); for(i;i<102;i++){ arr[nums[i]]++; } for(i = 0;i<102;i++){ if(arr[i] == 1){ res += 1; } } return res; }直接上结果
-
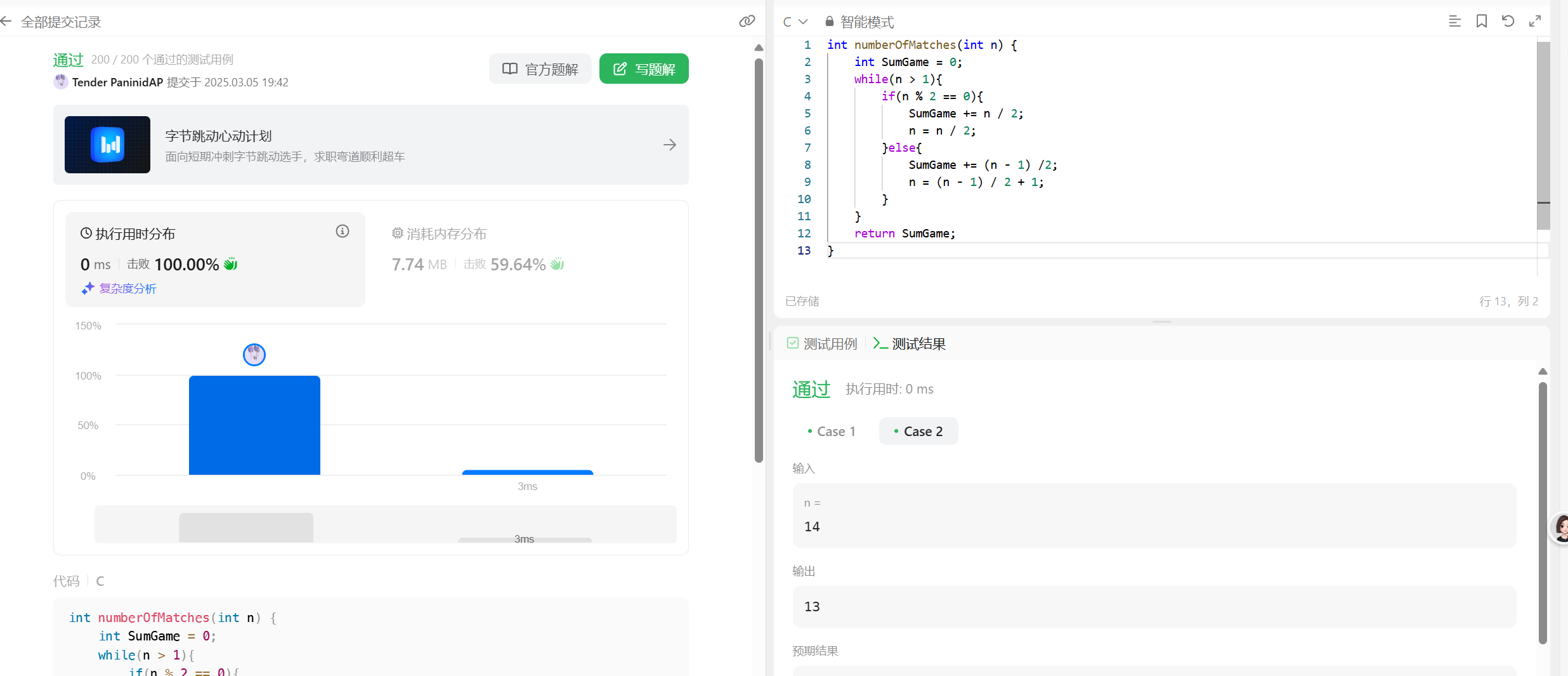
力扣1688比赛中的配对次数 太简单了，直接上题目和代码给你一个整数 n ，表示比赛中的队伍数。比赛遵循一种独特的赛制：如果当前队伍数是 偶数 ，那么每支队伍都会与另一支队伍配对。总共进行 n / 2 场比赛，且产生 n / 2 支队伍进入下一轮。如果当前队伍数为 奇数 ，那么将会随机轮空并晋级一支队伍，其余的队伍配对。总共进行 (n - 1) / 2 场比赛，且产生 (n - 1) / 2 + 1 支队伍进入下一轮。返回在比赛中进行的配对次数，直到决出获胜队伍为止。示例 1：输入：n = 7输出：6解释：比赛详情：第 1 轮：队伍数 = 7 ，配对次数 = 3 ，4 支队伍晋级。第 2 轮：队伍数 = 4 ，配对次数 = 2 ，2 支队伍晋级。第 3 轮：队伍数 = 2 ，配对次数 = 1 ，决出 1 支获胜队伍。总配对次数 = 3 + 2 + 1 = 6示例 2：输入：n = 14输出：13解释：比赛详情：第 1 轮：队伍数 = 14 ，配对次数 = 7 ，7 支队伍晋级。第 2 轮：队伍数 = 7 ，配对次数 = 3 ，4 支队伍晋级。第 3 轮：队伍数 = 4 ，配对次数 = 2 ，2 支队伍晋级。第 4 轮：队伍数 = 2 ，配对次数 = 1 ，决出 1 支获胜队伍。总配对次数 = 7 + 3 + 2 + 1 = 13提示：1 <= n <= 200直接上代码int numberOfMatches(int n) { int SumGame = 0; while(n > 1){ if(n % 2 == 0){ SumGame += n / 2; n = n / 2; }else{ SumGame += (n - 1) /2; n = (n - 1) / 2 + 1; } } return SumGame; }简直无脑
-
大模型中的 Token：AI 语言魔法的关键解码器 在自然语言处理（NLP）的大模型中，Token 是一个核心概念。理解 Token 对于解读模型的工作原理、训练机制以及生成内容的方式至关重要。本文将从基础入手，逐步深入地介绍 Token 的定义、作用、以及在大模型中的具体应用。什么是 Token？基本定义Token 是对文本进行分解后形成的最小单位。它可以是：单个字符：如a，b。一个词：如hello，world。一个子词：如un-（前缀），-ing（后缀）。标点符号：如,，.。特殊符号：如（结束符），（未知词）。Token 与字和词的关系Token 不等同于字或词，而是一种介于两者之间的处理方式。例如：在英文中，running可能被分解为run和ing。在中文中，自然语言处理通常会按词分解为自然、语言和处理，也可能直接用字符作为 Token。为什么需要 Token？语言是连续的，而模型需要离散的输入。Token 的引入是为了将语言映射到可以被机器理解的离散数据形式，方便处理和学习。Token 在大模型中的作用输入编码在处理自然语言时，原始文本首先被分解成一系列 Token，然后被编码为数字 ID（通常是整数），以便输入模型。例如：原始文本：I love AI.Token 化：("I","love","AI",".")编码：(101,1567,7896,102)训练与预测大模型通过学习 Token 的分布规律，预测下一个 Token 或生成新的句子。以下是两个典型应用：语言建模：根据前面的 Token 序列，预测下一个 Token。生成任务：根据输入的 Token 序列，生成满足任务要求的输出文本。控制序列长度Token 的数量直接影响模型的性能和计算开销。例如，GPT 模型有最大 Token 限制（如 4096 tokens），这决定了它能处理的上下文长度。Token 的分解方式：分词算法详解为了将文本分解为 Token，需要使用特定的分词算法。以下是几种常见方法：基于规则的分词最简单的方式，按空格或标点直接拆分。例如：输入：I love programming.输出：("I","love","programming",".")Byte-Pair Encoding（BPE）BPE 是一种基于统计的子词分词方法，广泛用于 GPT 系列模型：将文本初始化为单字符序列。找到出现频率最高的字符对，合并为新 Token。重复步骤，直到达到预定 Token 数量。例子：输入：low，lower，lowest初始 Token：("l","o","w","l","o","w","e","r","l","o","w","e","s","t")经过多轮合并后：("low","lower","lowest")SentencePieceSentencePiece 是一种模型无关的分词器，可以直接处理未分词的文本。它使用 BPE 或 Unigram 算法进行分词，适用于多种语言。WordPiece与 BPE 类似，但主要用于 BERT 模型。它会优先生成常见词作为 Token，同时允许不常见词分解为更小的子词。Token 在大模型中的结构与优化Embedding 表每个 Token 都对应一个向量表示，存储在模型的嵌入层（Embedding layer）中。嵌入层的作用是将离散的 Token 映射到连续的向量空间。模型层的作用编码器（Encoder）：处理输入 Token，生成上下文相关的表示。解码器（Decoder）：根据编码器输出和历史 Token，生成下一个 Token。Token 优化为了提升效率和准确性，研究人员会优化 Token 的设计和处理：减少无用 Token：如避免将常见标点符号频繁拆分。增加子词共享：通过共享 Token 表，提升跨任务的泛化能力。上下文压缩：通过合并低频 Token，减少 Token 总数。与 Token 相关的实际问题与挑战长序列问题长文本会生成更多的 Token，导致计算成本增加。这对上下文较长的任务（如总结长文章）是一个挑战。多语言适配不同语言的分词方式差异显著，需要设计统一的 Token 化方法。例如，中文需要按字分解，而阿拉伯语需要考虑词形变化。未知 Token 的处理模型可能遇到未在训练中见过的词。这时会用特殊 Token替代，可能降低生成内容的流畅性。Token 的未来展望随着模型能力的提升，Token 的设计也在不断演进：动态分词根据任务动态调整 Token 化方式，兼顾精度和效率。超长上下文通过压缩 Token 或改进架构，处理更长的输入序列。多模态 Token将文字、图像等统一编码为 Token，支持多模态任务。结语Token 是大模型中最基本却至关重要的组成部分。从文本分解到生成语言，Token 的处理贯穿始终。了解 Token 的原理和应用，不仅有助于深入理解大模型的工作机制，还能为其进一步优化和应用提供理论支持。
