搜索到
64
篇与
的结果
-
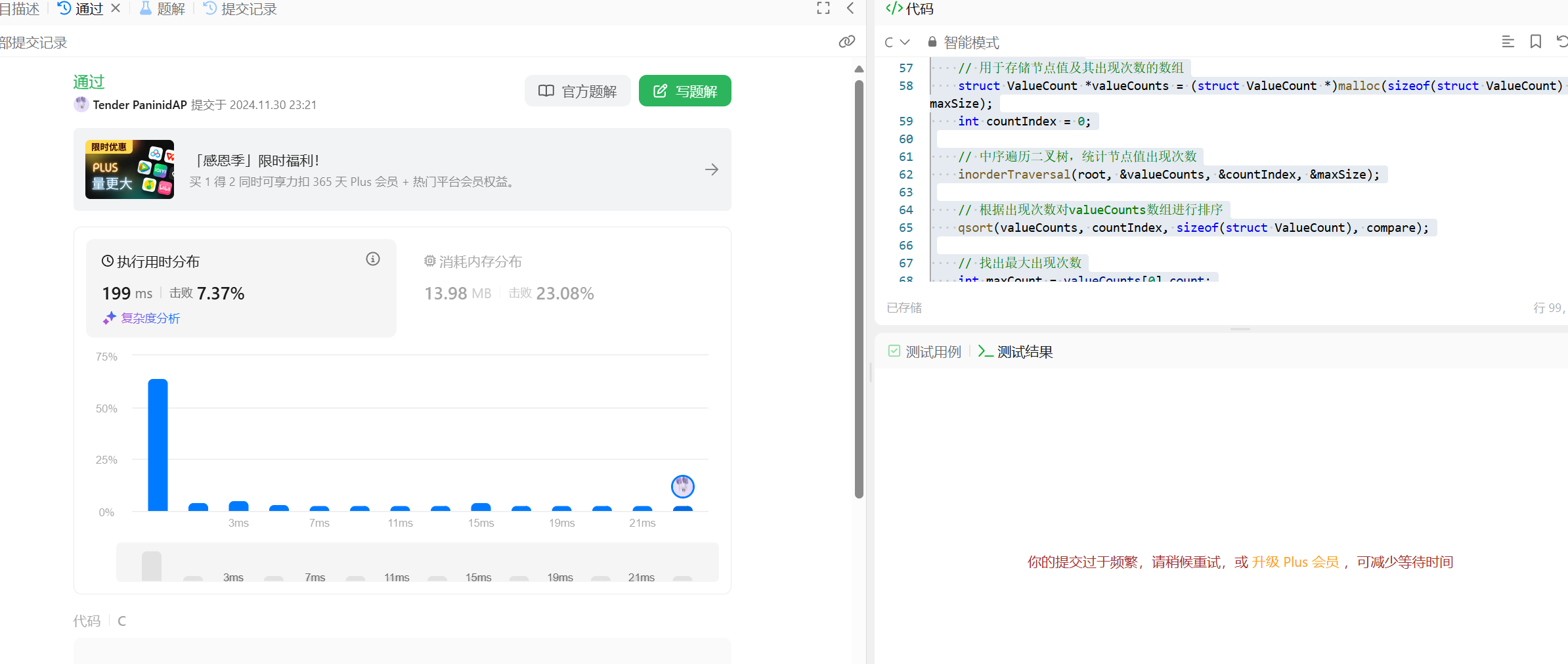
力扣 二叉搜索树中的众树 给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。如果树中有不止一个众数，可以按 任意顺序 返回。假定 BST 满足如下定义：结点左子树中所含节点的值 小于等于 当前节点的值结点右子树中所含节点的值 大于等于 当前节点的值左子树和右子树都是二叉搜索树上代码 // 比较函数，用于qsort int compare(const void * a, const void * b) { struct ValueCount *va = (struct ValueCount *)a; struct ValueCount *vb = (struct ValueCount *)b; return vb->count - va->count; } // 中序遍历二叉树，统计每个节点值的出现次数 void inorderTraversal(struct TreeNode *node, struct ValueCount **valueCounts, int *countIndex, int *maxSize) { if (node == NULL) { return; } inorderTraversal(node->left, valueCounts, countIndex, maxSize); int i; for (i = 0; i < *countIndex; i++) { if ((*valueCounts)[i].value == node->val) { (*valueCounts)[i].count++; break; } } if (i == *countIndex) { // 检查是否需要扩容数组 if (*countIndex >= *maxSize) { // 扩容策略，这里简单地翻倍 *maxSize *= 2; struct ValueCount *newArray = (struct ValueCount *)realloc(*valueCounts, sizeof(struct ValueCount) * (*maxSize)); if (newArray == NULL) { // 处理内存分配失败的情况 printf("内存分配失败！\n"); exit(1); } *valueCounts = newArray; } (*valueCounts)[*countIndex].value = node->val; (*valueCounts)[*countIndex].count = 1; (*countIndex)++; } inorderTraversal(node->right, valueCounts, countIndex, maxSize); } // 找出众数并返回结果数组 int *findMode(struct TreeNode *root, int *returnSize) { // 初始分配足够的空间，这里假设初始大小为10 int maxSize = 10; // 用于存储节点值及其出现次数的数组 struct ValueCount *valueCounts = (struct ValueCount *)malloc(sizeof(struct ValueCount) * maxSize); int countIndex = 0; // 中序遍历二叉树，统计节点值出现次数 inorderTraversal(root, &valueCounts, &countIndex, &maxSize); // 根据出现次数对valueCounts数组进行排序 qsort(valueCounts, countIndex, sizeof(struct ValueCount), compare); // 找出最大出现次数 int maxCount = valueCounts[0].count; // 统计众数的个数 int modeCount = 0; for (int i = 0; i < countIndex; i++) { if (valueCounts[i].count == maxCount) { modeCount++; } else { break; } } // 分配返回结果数组的空间 int *modes = (int *)malloc(sizeof(int) * modeCount); // 将众数填充到返回结果数组中 int j = 0; for (int i = 0; i < countIndex && j < modeCount; i++) { if (valueCounts[i].count == maxCount) { modes[j] = valueCounts[i].value; j++; } } // 释放用于统计节点值出现次数的数组空间 free(valueCounts); // 设置返回结果数组的大小 *returnSize = modeCount; return modes; }思路很简单，思路就是先把树进行一个中序排序，接下来进行把一个一个数字都放到哈希表里面，然后一个一个循环哈希表里面的数字，进行排序。选出一个最大的来，思路就是这个样子 -
力扣350俩个数组的交集Ⅱ 给你两个整数数组 nums1 和 nums2 ，请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序。上代码int* intersect(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize){ int table[1001]; int count=0; int* ans=(int*)malloc(sizeof(int)*nums2Size); memset(table,0,sizeof(table)); for(int i=0;i<nums1Size;i++){ table[nums1[i]]+=1; } for(int i=0;i<nums2Size;i++){ if(table[nums2[i]]>0){ ans[count++]=nums2[i]; table[nums2[i]]-=1; } } *returnSize=count; return ans; } 最悲催的一次
-
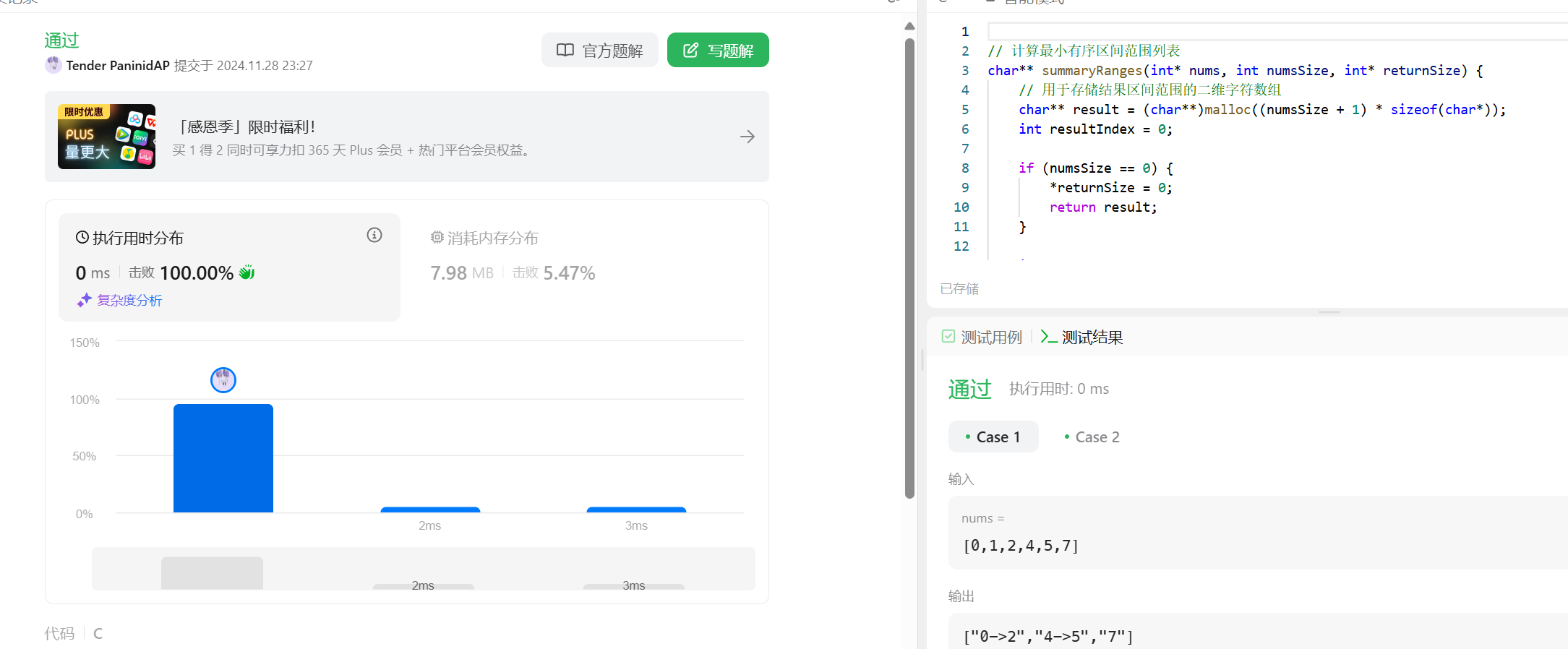
力扣288和汇总区间 给定一个 无重复元素 的 有序 整数数组 nums 。返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说，nums 的每个元素都恰好被某个区间范围所覆盖，并且不存在属于某个范围但不属于 nums 的数字 x 。列表中的每个区间范围 [a,b] 应该按如下格式输出："a->b" ，如果 a != b"a" ，如果 a == b我用的哈希的做法上答案我看其他人没有人用哈希的，感觉就我一个人。。。#include <stdio.h> #include <stdlib.h> #include <string.h> // 计算最小有序区间范围列表 char** summaryRanges(int* nums, int numsSize, int* returnSize) { // 用于存储结果区间范围的二维字符数组 char** result = (char**)malloc((numsSize + 1) * sizeof(char*)); int resultIndex = 0; if (numsSize == 0) { *returnSize = 0; return result; } int start = nums[0]; int end = nums[0]; for (int i = 1; i < numsSize; i++) { if (nums[i] == end + 1) { end = nums[i]; } else { // 生成当前区间范围的字符串并存储到结果数组 if (start == end) { result[resultIndex] = (char*)malloc(20 * sizeof(char)); sprintf(result[resultIndex], "%d", start); } else { result[resultIndex] = (char*)malloc(40 * sizeof(char)); sprintf(result[resultIndex], "%d->%d", start, end); } resultIndex++; start = nums[i]; end = nums[i]; } } // 处理最后一个区间范围 if (start == end) { result[resultIndex] = (char*)malloc(20 * sizeof(char)); sprintf(result[resultIndex], "%d", start); } else { result[resultIndex] = (char*)malloc(40 * sizeof(char)); sprintf(result[resultIndex], "%d->%d", start, end); } resultIndex++; *returnSize = resultIndex; return result; }
-
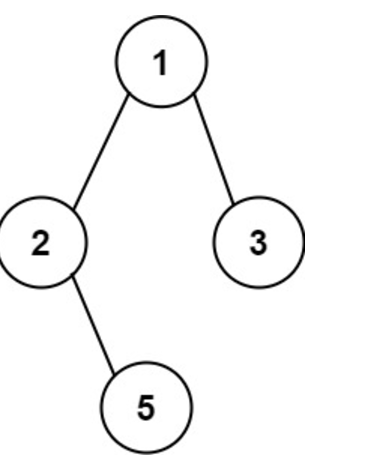
日更力扣257二叉树的所有路径 还是老规矩上题目给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。示例 1：输入：root = [1,2,3,null,5]输出：["1->2->5","1->3"]示例 2：输入：root = [1]输出：["1"]接下来上代码void cons_paths(struct TreeNode* root,char** ss,int* stack,int top,int* returnSize){ if(root == NULL){ return; }else{ if(root->left != NULL || root->right !=NULL){ stack[top] = root -> val; top++; cons_paths(root->left,ss,stack,top,returnSize); cons_paths(root->right,ss,stack,top,returnSize); }else{ char* s = (char*)malloc(sizeof(int) * 500); int len = 0; int i = 0; for(i;i<top;i++){ len = len + sprintf(s + len,"%d->",stack[i]); } sprint(s+len,"%d->",root->val); ss[(*returnSize)] = s; (*returnSize)++; } } } char** binaryTreePaths(struct TreeNode* root, int* returnSize) { char** ss = (char**)malloc(sizeof(char*) * 100); *returSize = 0; int stack[100]; cons_paths(root,ss,stack,0,returnSize); return ss; }思路来源于某大佬，他大概意思是这样的，先进性一个stack 把一条路线是的所有都是传到一个stack里面 然后再一个一个拿数组里面来，先写这些，明天好好的吧全部的思路解释清楚
-
学习了一下新的一个大型一点的写法 用队列实现栈请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。实现 MyStack 类：void push(int x) 将元素 x 压入栈顶。int pop() 移除并返回栈顶元素。int top() 返回栈顶元素。boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。代码如下 #define LEN 20 typedef struct queue { int *data; int head; int rear; int size; } Queue; typedef struct { Queue *queue1, *queue2; } MyStack; Queue *initQueue(int k) { Queue *obj = (Queue *)malloc(sizeof(Queue)); obj->data = (int *)malloc(k * sizeof(int)); obj->head = -1; obj->rear = -1; obj->size = k; return obj; } void enQueue(Queue *obj, int e) { if (obj->head == -1) { obj->head = 0; } obj->rear = (obj->rear + 1) % obj->size; obj->data[obj->rear] = e; } int deQueue(Queue *obj) { int a = obj->data[obj->head]; if (obj->head == obj->rear) { obj->rear = -1; obj->head = -1; return a; } obj->head = (obj->head + 1) % obj->size; return a; } int isEmpty(Queue *obj) { return obj->head == -1; } MyStack *myStackCreate() { MyStack *obj = (MyStack *)malloc(sizeof(MyStack)); obj->queue1 = initQueue(LEN); obj->queue2 = initQueue(LEN); return obj; } void myStackPush(MyStack *obj, int x) { if (isEmpty(obj->queue1)) { enQueue(obj->queue2, x); } else { enQueue(obj->queue1, x); } } int myStackPop(MyStack *obj) { if (isEmpty(obj->queue1)) { while (obj->queue2->head != obj->queue2->rear) { enQueue(obj->queue1, deQueue(obj->queue2)); } return deQueue(obj->queue2); } while (obj->queue1->head != obj->queue1->rear) { enQueue(obj->queue2, deQueue(obj->queue1)); } return deQueue(obj->queue1); } int myStackTop(MyStack *obj) { if (isEmpty(obj->queue1)) { return obj->queue2->data[obj->queue2->rear]; } return obj->queue1->data[obj->queue1->rear]; } bool myStackEmpty(MyStack *obj) { if (obj->queue1->head == -1 && obj->queue2->head == -1) { return true; } return false; } void myStackFree(MyStack *obj) { free(obj->queue1->data); obj->queue1->data = NULL; free(obj->queue1); obj->queue1 = NULL; free(obj->queue2->data); obj->queue2->data = NULL; free(obj->queue2); obj->queue2 = NULL; free(obj); obj = NULL; }解释如下以下是对这段代码的详细解释：1. 宏定义和结构体定义#define LEN 20这行代码定义了一个宏 LEN，其值为 20。在后续代码中，这个宏可以被用来表示一个固定的长度值，例如用于初始化队列的容量等，通过使用宏可以方便地在一处修改这个长度值，而不需要在多处代码中逐个修改具体的数字。typedef struct queue { int *data; int head; int rear; int size; } Queue;这里定义了一个名为 Queue 的结构体。结构体中包含以下成员：int *data：一个指向整数类型的指针，用于存储队列中的数据元素。int head：表示队列头部的索引，用于标记队列头部元素的位置。int rear：表示队列尾部的索引，用于标记队列尾部元素的位置。int size：表示队列的容量大小，即可以存储的元素个数。typedef struct { Queue *queue1, *queue2; } MyStack;定义了一个名为 MyStack 的结构体，它包含两个指向 Queue 结构体的指针 queue1 和 queue2。这个结构体将用于实现一个栈的数据结构，通过两个队列来模拟栈的操作。2. 队列相关操作函数2.1 initQueue 函数Queue *initQueue(int k) { Queue *obj = (Queue *)malloc(sizeof(Queue)); obj->data = (int *)malloc(k * sizeof(int)); obj->head = -1; obj->rear = -1; obj->size = k; return obj; }这个函数用于初始化一个队列。它接受一个整数参数 k，用于指定队列的容量大小。函数内部的操作如下：首先，通过 malloc 函数动态分配内存来创建一个 Queue 结构体对象，并将其指针赋值给 obj。然后，再次使用 malloc 函数为队列的数据存储区域（data 指针所指向的区域）分配足够的内存空间，以存储 k 个整数类型的数据元素。接着，将队列的头部索引 head 和尾部索引 rear 都初始化为 -1，表示队列初始为空。最后，将队列的容量大小 size 设置为传入的参数 k，并返回初始化好的队列对象指针 obj。2.2 enQueue 函数void enQueue(Queue *obj, int e) { if (obj->head == -1) { obj->head = 0; } obj->rear = (obj->rear + 1) % obj->size; obj->data[obj->rear] = e; }该函数用于向队列中插入一个元素。它接受一个指向 Queue 结构体的指针 obj 和一个整数元素 e 作为参数。具体操作如下：首先，如果队列的头部索引 head 为 -1，说明队列当前为空，那么将头部索引 head 设置为 0，表示队列即将插入第一个元素。然后，通过 (obj->rear + 1) % obj->size 的方式计算新的尾部索引 rear。这种取模运算的方式实现了循环队列的效果，当队列尾部到达数组末尾时，会自动循环回到数组开头继续插入元素。最后，将传入的元素 e 存储到队列数据数组中由新的尾部索引 rear 所指向的位置。2.3 deQueue 函数int deQueue(Queue *obj) { int a = obj->data[obj->head]; if (obj->head == obj->rear) { obj->rear = -1; obj->head = -1; return a; } obj->head = (obj->head + 1) % obj->size; return a; }这个函数用于从队列中删除并返回头部的元素。它接受一个指向 Queue 结构体的指针 obj 作为参数。操作步骤如下：首先，取出队列头部索引 head 所指向的数据元素，并将其存储到变量 a 中。然后，判断如果队列的头部索引 head 和尾部索引 rear 相等，说明队列中只剩下一个元素，此时将头部索引 head 和尾部索引 rear 都重新设置为 -1，表示队列再次变为空。否则，如果队列中还有多个元素，就通过 (obj->head + 1) % obj->size 的方式更新头部索引 head，使其指向下一个元素，实现删除头部元素的效果。最后，返回之前取出的头部元素 a。2.4 isEmpty 函数int isEmpty(Queue *obj) { return obj->head == -1; }这个函数用于判断队列是否为空。它接受一个指向 Queue 结构体的指针 obj 作为参数，通过检查队列的头部索引 head 是否为 -1 来判断队列是否为空，如果 head 为 -1，则表示队列中没有元素，函数返回 1（在C语言中，非零值表示真），否则返回 0（表示假）。3. 栈相关操作函数3.1 myStackCreate 函数MyStack *myStackCreate() { MyStack *obj = (MyStack *)malloc(sizeof(MyStack)); obj->queue1 = initQueue(LEN); obj->queue2 = initQueue(LEN); return obj; }这个函数用于创建一个模拟栈的数据结构对象。它首先通过 malloc 函数动态分配内存来创建一个 MyStack 结构体对象，并将其指针赋值给 obj。然后，分别调用 initQueue 函数初始化 obj 结构体中的两个队列 queue1 和 queue2，并将它们的指针赋值给对应的成员变量。最后，返回创建好的模拟栈对象指针 obj。3.2 myStackPush 函数void myStackPush(MyStack *obj, int x) { if (isEmpty(obj->queue1)) { enQueue(obj->queue2, x); } else { enQueue(obj->queue2, x); } }该函数用于向模拟栈中压入一个元素。它接受一个指向 MyStack 结构体的指针 obj 和一个整数元素 x 作为参数。函数通过检查 obj 结构体中的队列 queue1 是否为空来决定将元素压入哪个队列。如果 queue1 为空，就将元素 x 压入队列 queue2；否则，将元素 x 压入队列 queue1。3.3 myStackPop 函数int myStackPop(MyStack *obj) { if (isEmpty(obj->queue1)) { while (obj->queue2->head!= obj->queue2->rear) { enQueue(obj->queue1, deQueue(obj->queue2)); } return deQueue(obj->queue2); } while (obj->queue1->head!= obj->queue1->rear) { enQueue(obj->queue2, deQueue(obj->queue1)); } return deQueue(obj->queue1); }这个函数用于从模拟栈中弹出一个元素。它接受一个指向 MyStack 结构体的指针 obj 作为参数。函数首先判断队列 queue1 是否为空，如果为空，则将队列 queue2 中的元素除了最后一个之外全部转移到队列 queue1 中，然后弹出队列 queue2 的最后一个元素并返回；如果队列 queue1 不为空，则将队列 queue1 中的元素除了最后一个之外全部转移到队列 queue2 中，然后弹出队列 queue1 的最后一个元素并返回。通过这种方式实现了模拟栈的弹出操作，使得每次弹出的元素都是最后压入的元素。3.4 myStackTop 函数int myStackTop(MyStack *obj) { if (isEmpty(obj->queue1)) { return obj->queue2->data[obj->queue2->rear]; } return obj->queue1->data[obj->queue1->rear]; }该函数用于获取模拟栈的栈顶元素。它接受一个指向 MyStack 结构体的指针 obj 作为参数。函数通过检查队列 queue1 是否为空来决定返回哪个队列的尾部元素作为栈顶元素。如果 queue1 为空，则返回队列 queue2 的尾部元素；否则，返回队列 queue1 的尾部元素。3.5 myStackEmpty 函数bool myStackEmpty(MyStack *obj) { if (obj->queue1->head == -1 && obj->queue2->head == -1) { return true; } return false; }这个函数用于判断模拟栈是否为空。它接受一个指向 MyStack 结构体的指针 obj 作为参数。通过检查 obj 结构体中的两个队列 queue1 和 queue2 的头部索引是否都为 -1 来判断模拟栈是否为空。如果两个队列的头部索引都为 -1，则表示模拟栈中没有元素，函数返回 true；否则，返回 false。3.6 myStackFree 函数void myStackFree(MyStack *obj) { free(obj->queue1->data); obj->queue1->data = NULL; free(obj->queue1); obj->queue1 = NULL; free(obj->queue2->data); obj->queue2->data = NULL; free(obj->queue2); obj->queue2 = NULL; free(obj); obj = NULL; }这个函数用于释放模拟栈所占用的内存资源。它接受一个指向 MyStack 结构体的指针 obj 作为参数。函数首先释放两个队列 queue1 和 queue2 中数据存储区域的内存，然后将对应的 data 指针设置为 NULL，以避免悬空指针。接着，释放两个队列结构体本身的内存，并将队列指针设置为 NULL。最后，释放模拟栈结构体 MyStack 本身的内存，并将模拟栈指针 obj 设置为 NULL，确保所有相关内存都被正确释放，防止内存泄漏。
