搜索到
15
篇与
的结果
-
域名做新站：站在巨人肩膀上的 SEO 捷径 老域名做新站：站在巨人肩膀上的SEO捷径在数字化浪潮席卷的今天，网站建设早已从"域名注册-内容填充-等待流量"的简单模式，演变为需要深度策略的系统性工程。对于追求快速见效的站长而言，老域名的价值正在被重新定义——它不仅是一串字符的组合，更是承载着搜索引擎信任、历史数据和潜在流量的"数字资产"。本文将深度解析老域名在新站建设中的核心优势，并提供实操建议，助您避开陷阱，最大化发挥老域名的效能。一、搜索引擎信任度：天然的"免死金牌"搜索引擎对网站的信任度评估，如同人类社会的"信用评分"，是长期积累的结果。老域名的注册年限直接影响着这一评分体系：沙盒期缩短：新站通常需要经历3-6个月的"沙盒期"，期间搜索引擎会对网站进行严格考核。而老域名凭借其历史记录，能快速通过基础信任验证，部分案例显示，优质老域名可将沙盒期缩短至1个月内。抗风险能力：在算法频繁更新的背景下，老域名因长期稳定存在，更容易适应规则变化。某电商平台曾用10年老域名重建新站，在经历Google Penguin算法更新时，排名波动仅为同类新站的1/3。案例佐证：某科技博客使用7年老域名（原为服装行业）搭建新站，上线3天内即收录全部内容页，核心关键词排名进入前10，而同期新域名站点仍处于沙盒考核阶段。二、历史数据赋能：隐形的流量引擎老域名的价值不仅在于年龄，更在于其沉淀的"数字遗产"：外链资源继承：即使原网站已关闭，老域名的外链网络仍可能持续发挥作用。某SEO团队通过工具监测发现，一个5年老域名的反向链接中，有32%仍能为新站带来蜘蛛抓取。历史内容权重：若老域名曾被高质量内容填充，其页面在搜索引擎中的"质量印记"可能延续。例如，某教育类老域名转向电商后，其原有的课程页面仍能为新站带来长尾流量。蜘蛛抓取优先级：搜索引擎会根据域名历史调整抓取频率。实验数据显示，使用老域名的新站，蜘蛛首次访问时间平均比新域名快4.7小时。三、域名类型溢价：特殊后缀的权重加持域名后缀的选择往往被低估，而实际上不同类型后缀在搜索引擎中享受差异化待遇：.edu/.gov后缀：这类域名因具有权威性，通常获得额外信任加分。某高校实验室使用.edu域名搭建的新站，在未做外链的情况下，核心关键词排名直接进入前5。行业专属后缀：如.tech、.health等，可强化领域相关性。某医疗资讯平台通过收购.health老域名，使专业内容的收录速度提升40%。通用顶级域名：.com/.net等老牌后缀依然占据流量优势，尤其在跨语言搜索场景中表现突出。四、品牌与流量红利：降低冷启动成本老域名的品牌价值往往被忽视，但却是新站快速获客的关键：记忆成本优势：研究表明，用户对老域名的信任度比新域名高27%，更易产生点击行为。历史流量继承：部分老域名可能携带未完全流失的直接访问流量。某旅游论坛通过收购过期域名，意外获得日均300+的自然流量。社交传播优势：在社交媒体分享时，老域名更易被用户接受，降低链接被标记为垃圾的风险。五、避坑指南：如何挑选高价值老域名历史清白验证：使用Ahrefs/Majestic等工具核查域名是否有处罚记录、垃圾外链或灰色行业关联。行业相关性匹配：优先选择与新站主题相近的老域名，如电商类新站应偏向零售、物流等领域的历史记录。数据指标筛选：重点关注：域名年龄（建议5年以上）历史最高权重（DA/PA值）自然外链数量与质量收录量与关键词排名表现价格与风险平衡：优质老域名价格从数百到数万不等，需结合预算与预期收益进行评估。结语：老域名不是万能药，却是加速器在SEO领域，"内容为王"的铁律从未改变，但老域名能为优质内容提供更高效的传播通道。它如同赛车的涡轮增压系统，让新站在竞争中获得先发优势。然而，选择老域名如同投资古董，需兼具专业眼光与风险意识。唯有将老域名的历史积淀与新站的创新内容深度融合，才能真正实现"站在巨人肩膀上"的飞跃。未来，随着搜索引擎算法的持续进化，老域名的价值可能会呈现新的维度。但可以确定的是，在可预见的未来，它仍将是数字资产配置中的重要一环。 -
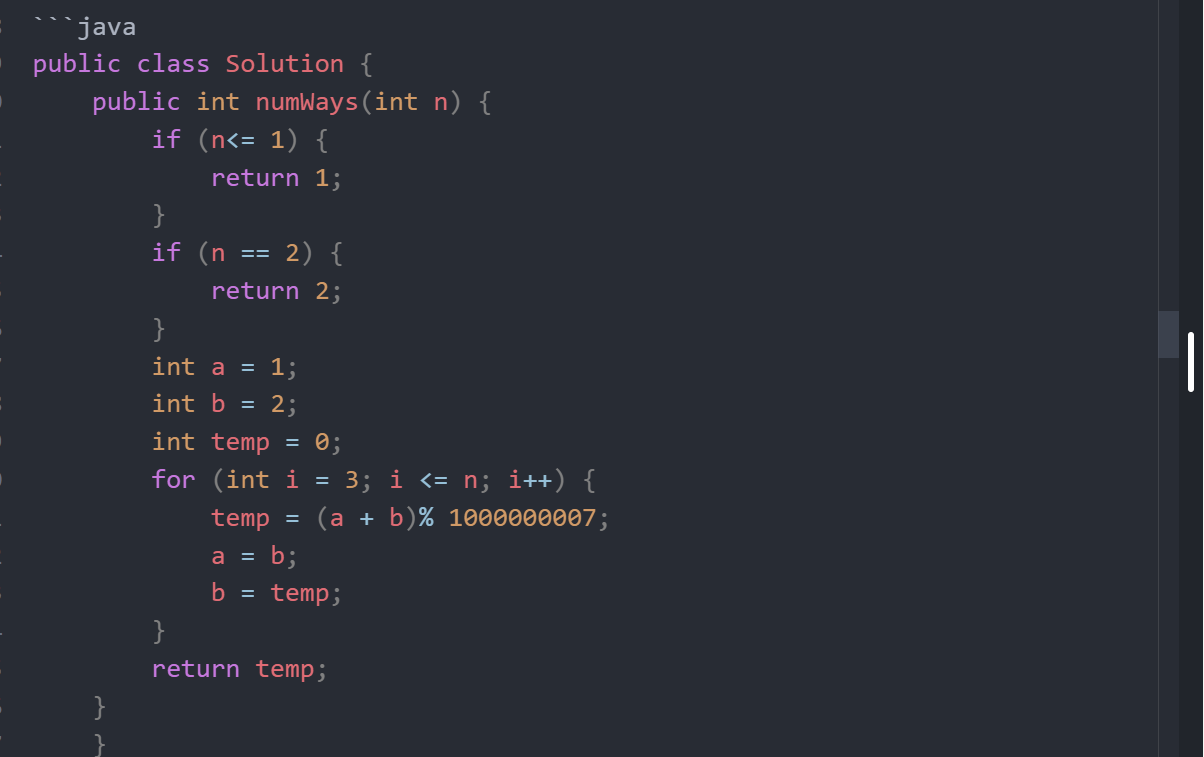
每日一个算法思想 - 动态规划（DP） 今天了解的算法思想的动态规划，这个内容算是算法里面比较重要的内容了。动态规划的英文名字叫做 Dynamic programming 这个不重要 直接学习思想简单来说就是拆分子问题，记住过往，减少重复计算量,接下来我将会举一个例子，让你快速理解说明是动态规划的含义。A ： "1+1+1+1+1+1+1+1 =？"A ： "上面等式的值是多少"B ： 计算 "8"A : 在上面等式的左边写上 "1+" 呢？A : "此时等式的值为多少"B : 很快得出答案 "9"A : "你怎么这么快就知道答案了"A : "只要在8的基础上加1就行了"A : "所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"上面就是一个简单的例子说明所以说上面看明白了吗一个例子带你走进动态规划 -- 青蛙跳阶问题暴力递归★ leetcode原题：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。”有些小伙伴第一次见这个题的时候，可能会有点蒙圈，不知道怎么解决。其实可以试想：★要想跳到第10级台阶，要么是先跳到第9级，然后再跳1级台阶上去;要么是先跳到第8级，然后一次迈2级台阶上去。同理，要想跳到第9级台阶，要么是先跳到第8级，然后再跳1级台阶上去;要么是先跳到第7级，然后一次迈2级台阶上去。要想跳到第8级台阶，要么是先跳到第7级，然后再跳1级台阶上去;要么是先跳到第6级，然后一次迈2级台阶上去。”假设跳到第n级台阶的跳数我们定义为f(n)，很显然就可以得出以下公式：f（10） = f（9）+f(8)f (9) = f(8) + f(7)f (8) = f(7) + f(6)...f(3) = f(2) + f(1)即通用公式为: f(n) = f(n-1) + f(n-2)那f(2) 或者 f(1) 等于多少呢？当只有2级台阶时，有两种跳法，第一种是直接跳两级，第二种是先跳一级，然后再跳一级。即f(2) = 2;当只有1级台阶时，只有一种跳法，即f（1）= 1；因此可以用递归去解决这个问题：class Solution {public int numWays(int n) { if(n == 1){ return 1; } if(n == 2){ return 2; } return numWays(n-1) + numWays(n-2); }}去leetcode提交一下，发现有问题，超出时间限制了为什么超时了呢？递归耗时在哪里呢？先画出递归树看看：要计算原问题 f(10)，就需要先计算出子问题 f(9) 和 f(8)然后要计算 f(9)，又要先算出子问题 f(8) 和 f(7)，以此类推。一直到 f(2) 和 f(1），递归树才终止。我们先来看看这个递归的时间复杂度吧：递归时间复杂度 = 解决一个子问题时间*子问题个数一个子问题时间 = f（n-1）+f（n-2），也就是一个加法的操作，所以复杂度是 O(1)；问题个数 = 递归树节点的总数，递归树的总节点 = 2^n-1，所以是复杂度O(2^n)。因此，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n)，就是指数级别的，爆炸增长的，如果n比较大的话，超时很正常的了。回过头来，你仔细观察这颗递归树，你会发现存在大量重复计算，比如f（8）被计算了两次，f（7）被重复计算了3次...所以这个递归算法低效的原因，就是存在大量的重复计算！既然存在大量重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去备忘录查一下，如果有，就直接取就好了，备忘录没有才开始计算，那就可以省去重新重复计算的耗时啦！这就是带备忘录的解法。带备忘录的递归解法（自顶向下）一般使用一个数组或者一个哈希map充当这个备忘录。第一步，f（10）= f(9) + f(8)，f(9) 和f（8）都需要计算出来，然后再加到备忘录中，如下：第二步， f(9) = f（8）+ f（7），f（8）= f（7）+ f(6), 因为 f(8) 已经在备忘录中啦，所以可以省掉，f(7),f（6）都需要计算出来，加到备忘录中~第三步， f(8) = f（7）+ f(6),发现f(8)，f(7),f（6）全部都在备忘录上了，所以都可以剪掉。所以呢，用了备忘录递归算法，递归树变成光秃秃的树干咯，如下：带备忘录的递归算法，子问题个数=树节点数=n，解决一个子问题还是O(1),所以带备忘录的递归算法的时间复杂度是O(n)。接下来呢，我们用带备忘录的递归算法去撸代码，解决这个青蛙跳阶问题的超时问题咯~，代码如下：public class Solution { //使用哈希map，充当备忘录的作用 Map<Integer, Integer> tempMap = new HashMap(); public int numWays(int n) { // n = 0 也算1种 if (n == 0) { return 1; } if (n <= 2) { return n; } //先判断有没计算过，即看看备忘录有没有 if (tempMap.containsKey(n)) { //备忘录有，即计算过，直接返回 return tempMap.get(n); } else { // 备忘录没有，即没有计算过，执行递归计算,并且把结果保存到备忘录map中，对1000000007取余（这个是leetcode题目规定的） tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007); return tempMap.get(n); } } }去leetcode提交一下，如图，稳了：其实，还可以用动态规划解决这道题。自底向上的动态规划动态规划跟带备忘录的递归解法基本思想是一致的，都是减少重复计算，时间复杂度也都是差不多。但是呢：带备忘录的递归，是从f(10)往f(1）方向延伸求解的，所以也称为自顶向下的解法。动态规划从较小问题的解，由交叠性质，逐步决策出较大问题的解，它是从f(1)往f(10）方向，往上推求解，所以称为自底向上的解法。动态规划有几个典型特征，最优子结构、状态转移方程、边界、重叠子问题。在青蛙跳阶问题中：f(n-1)和f(n-2) 称为 f(n) 的最优子结构f(n)= f（n-1）+f（n-2）就称为状态转移方程f(1) = 1, f(2) = 2 就是边界啦比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。我们来看下自底向上的解法，从f(1)往f(10）方向，想想是不是直接一个for循环就可以解决啦，如下：带备忘录的递归解法，空间复杂度是O(n)，但是呢，仔细观察上图，可以发现，f（n）只依赖前面两个数，所以只需要两个变量a和b来存储，就可以满足需求了，因此空间复杂度是O(1)就可以啦动态规划实现代码如下：public class Solution { public int numWays(int n) { if (n<= 1) { return 1; } if (n == 2) { return 2; } int a = 1; int b = 2; int temp = 0; for (int i = 3; i <= n; i++) { temp = (a + b)% 1000000007; a = b; b = temp; } return temp; } }动态规划的解题套路什么样的问题可以考虑使用动态规划解决呢？★ 如果一个问题，可以把所有可能的答案穷举出来，并且穷举出来后，发现存在重叠子问题，就可以考虑使用动态规划。”比如一些求最值的场景，如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等，都是动态规划的经典应用场景。动态规划的解题思路动态规划的核心思想就是拆分子问题，记住过往，减少重复计算。 并且动态规划一般都是自底向上的，因此到这里，基于青蛙跳阶问题，我总结了一下我做动态规划的思路：穷举分析确定边界找出规律，确定最优子结构写出状态转移方程穷举分析当台阶数是1的时候，有一种跳法，f（1） =1当只有2级台阶时，有两种跳法，第一种是直接跳两级，第二种是先跳一级，然后再跳一级。即f(2) = 2;当台阶是3级时，想跳到第3级台阶，要么是先跳到第2级，然后再跳1级台阶上去，要么是先跳到第 1级，然后一次迈 2 级台阶上去。所以f(3) = f(2) + f(1) =3当台阶是4级时，想跳到第3级台阶，要么是先跳到第3级，然后再跳1级台阶上去，要么是先跳到第 2级，然后一次迈 2 级台阶上去。所以f(4) = f(3) + f(2) =5当台阶是5级时......确定边界通过穷举分析，我们发现，当台阶数是1的时候或者2的时候，可以明确知道青蛙跳法。f（1） =1，f(2) = 2，当台阶n>=3时，已经呈现出规律f(3) = f(2) + f(1) =3，因此f（1） =1，f(2) = 2就是青蛙跳阶的边界。找规律，确定最优子结构n>=3时，已经呈现出规律 f(n) = f(n-1) + f(n-2) ，因此，f(n-1)和f(n-2) 称为 f(n) 的最优子结构。什么是最优子结构？有这么一个解释：★ 一道动态规划问题，其实就是一个递推问题。假设当前决策结果是f(n),则最优子结构就是要让 f(n-k) 最优,最优子结构性质就是能让转移到n的状态是最优的,并且与后面的决策没有关系,即让后面的决策安心地使用前面的局部最优解的一种性质”4， 写出状态转移方程通过前面3步，穷举分析，确定边界，最优子结构，我们就可以得出状态转移方程啦：代码实现我们实现代码的时候，一般注意从底往上遍历哈，然后关注下边界情况，空间复杂度，也就差不多啦。动态规划有个框架的，大家实现的时候，可以考虑适当参考一下：dp0[...] = 边界值for(状态1 ：所有状态1的值){for(状态2 ：所有状态2的值){ for(...){ //状态转移方程 dp[状态1][状态2][...] = 求最值 } }}leetcode案例分析我们一起来分析一道经典leetcode题目吧★ 给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。”示例 1：输入：nums = [10,9,2,5,3,7,101,18]输出：4解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。示例 2：输入：nums = [0,1,0,3,2,3]输出：4我们按照以上动态规划的解题思路，穷举分析确定边界找规律，确定最优子结构状态转移方程1.穷举分析因为动态规划，核心思想包括拆分子问题，记住过往，减少重复计算。 所以我们在思考原问题：数组num[i]的最长递增子序列长度时，可以思考下相关子问题，比如原问题是否跟子问题num[i-1]的最长递增子序列长度有关呢？自顶向上的穷举这里观察规律，显然是有关系的，我们还是遵循动态规划自底向上的原则，基于示例1的数据，从数组只有一个元素开始分析。当nums只有一个元素10时，最长递增子序列是[10],长度是1.当nums需要加入一个元素9时，最长递增子序列是[10]或者[9],长度是1。当nums再加入一个元素2时，最长递增子序列是[10]或者[9]或者[2],长度是1。当nums再加入一个元素5时，最长递增子序列是[2,5],长度是2。当nums再加入一个元素3时，最长递增子序列是[2,5]或者[2,3],长度是2。当nums再加入一个元素7时，,最长递增子序列是[2,5,7]或者[2,3,7],长度是3。当nums再加入一个元素101时，最长递增子序列是[2,5,7,101]或者[2,3,7,101],长度是4。当nums再加入一个元素18时，最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4。当nums再加入一个元素7时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4.分析找规律，拆分子问题通过上面分析，我们可以发现一个规律：如果新加入一个元素nums[i], 最长递增子序列要么是以nums[i]结尾的递增子序列，要么就是nums[i-1]的最长递增子序列。看到这个，是不是很开心，nums[i]的最长递增子序列已经跟子问题 nums[i-1]的最长递增子序列有关联了。原问题数组nums[i]的最长递增子序列 = 子问题数组nums[i-1]的最长递增子序列/nums[i]结尾的最长递增子序列是不是感觉成功了一半呢？但是如何把nums[i]结尾的递增子序列也转化为对应的子问题呢？要是nums[i]结尾的递增子序列也跟nums[i-1]的最长递增子序列有关就好了。又或者nums[i]结尾的最长递增子序列，跟前面子问题num[j]（0=<j<i）结尾的最长递增子序列有关就好了，带着这个想法，我们又回头看看穷举的过程：nums[i]的最长递增子序列，不就是从以数组num[i]每个元素结尾的最长子序列集合，取元素最多（也就是长度最长）那个嘛，所以原问题，我们转化成求出以数组nums每个元素结尾的最长子序列集合，再取最大值嘛。哈哈，想到这，我们就可以用dp[i]表示以num[i]这个数结尾的最长递增子序列的长度啦，然后再来看看其中的规律：其实，nums[i]结尾的自增子序列，只要找到比nums[i]小的子序列，加上nums[i] 就可以啦。显然，可能形成多种新的子序列，我们选最长那个，就是dp[i]的值啦★nums[3]=5,以5结尾的最长子序列就是[2,5],因为从数组下标0到3遍历，只找到了子序列[2]比5小，所以就是[2]+[5]啦，即dp[4]=2nums[4]=3,以3结尾的最长子序列就是[2,3],因为从数组下标0到4遍历，只找到了子序列[2]比3小，所以就是[2]+[3]啦，即dp[4]=2nums[5]=7，以7结尾的最长子序列就是[2,5,7]和[2,3,7],因为从数组下标0到5遍历，找到2,5和3都比7小，所以就有[2,7],[5,7],[3,7],[2,5,7]和[2,3,7]这些子序列，最长子序列就是[2,5,7]和[2,3,7]，它俩不就是以5结尾和3结尾的最长递增子序列+[7]来的嘛！所以，dp[5]=3 =dp[3]+1=dp[4]+1。”很显然有这个规律：一个以nums[i]结尾的数组nums如果存在j属于区间[0，i-1],并且num[i]>num[j]的话，则有，dp(i) =max(dp(j))+1，最简单的边界情况当nums数组只有一个元素时，最长递增子序列的长度dp(1)=1,当nums数组有两个元素时，dp(2) =2或者1， 因此边界就是dp(1)=1。确定最优子结构从穷举分析，我们可以得出，以下的最优结构：dp(i) =max(dp(j))+1，存在j属于区间[0，i-1],并且num[i]>num[j]。max(dp(j)) 就是最优子结构。状态转移方程通过前面分析，我们就可以得出状态转移方程啦：所以数组num[i]的最长递增子序列就是：最长递增子序列 =max(dp[i])代码实现class Solution { public int lengthOfLIS(int[] nums) { if (nums.length == 0) { return 0; } int[] dp = new int[nums.length]; //初始化就是边界情况 dp[0] = 1; int maxans = 1; //自底向上遍历 for (int i = 1; i < nums.length; i++) { dp[i] = 1; //从下标0到i遍历 for (int j = 0; j < i; j++) { //找到前面比nums[i]小的数nums[j],即有dp[i]= dp[j]+1 if (nums[j] < nums[i]) { //因为会有多个小于nums[i]的数，也就是会存在多种组合了嘛，我们就取最大放到dp[i] dp[i] = Math.max(dp[i], dp[j] + 1); } } //求出dp[i]后，dp最大那个就是nums的最长递增子序列啦 maxans = Math.max(maxans, dp[i]); } return maxans; } }
-
优质RSS订阅地址-持续更新中 1.小海绵博客https://blog.wzl.icu/feed/知乎每日精选 https://www.zhihu.com/rss阮一峰的网络日志 https://www.ruanyifeng.com/blog/atom.xml阮一峰的网络日志 http://feeds.feedburner.com/ruanyifeng少数派 https://sspai.com/feed美团技术团队 https://rsshub.app/meituan/tech/homeV2EX https://v2ex.com/index.xml酷 壳 – CoolShell http://coolshell.cn/feed爱范儿 https://www.ifanr.com/feed知乎热榜 https://rsshub.app/zhihu/hotlist《联合早报》- 中港台 - 即时 https://plink.anyfeeder.com/zaobao/realtime/china南方周末 - 新闻 https://rsshub.app/infzm/2机核 https://www.gcores.com/rss奇客 Solidot–传递最新科技情报 https://www.solidot.org/index.rss热榜 - 煎蛋 https://rsshub.app/jandan/top《联合早报》- 国际 - 即时 https://plink.anyfeeder.com/zaobao/realtime/world「ONE・一个」 https://rsshub.app/one云风的 BLOG http://blog.codingnow.com/atom.xml知乎日报 https://rsshub.app/zhihu/daily小众软件 http://feed.appinn.com/抽屉新热榜 - 168 小时最热榜 https://rsshub.app/chouti/top/168极客公园 http://www.geekpark.net/rss构建我的被动收入 https://www.bmpi.dev/index.xml左岸读书 http://www.zreading.cn/feed掘金 前端 https://rsshub.app/juejin/category/frontend小众软件 https://www.appinn.com/feed/虎嗅网 https://www.huxiu.com/rss/0.xml36 氪 https://36kr.com/feed酷安 - 新鲜图文 https://rsshub.app/coolapk/tuwen-xinxian太隐 https://wangyurui.com/feed.xml异次元软件世界 http://feed.iplaysoft.com/DIYGod - 写代码是热爱，写到世界充满爱！ https://diygod.me/atom.xmlPython 工匠 https://www.zlovezl.cn/feeds/latest/王垠的博客 https://rsshub.app/blogs/wangyinbboysoul 的博客 https://www.bboy.app/atom.xml程序员的喵 https://catcoding.me/atom.xml虎嗅 https://rss.huxiu.com/微博热搜榜 https://rsshub.app/weibo/search/hot胡涂说 https://hutusi.com/feed.xml小众软件 https://feeds.appinn.com/appinns/土木坛子 https://tumutanzi.com/feed掘金专栏 - 字节跳动技术团队 https://rsshub.app/juejin/posts/1838039172387262开源中国 - 软件更新资讯 https://rsshub.app/oschina/news/project知乎日报 http://feeds.feedburner.com/zhihu-dailyoldj's blog https://oldj.net/feed每日一文 http://node2.feed43.com/mryw.xmlRandy's Blog https://lutaonan.com/rss.xmlhttps://draveness.me/feed.xml让小产品的独立变现更简单 - ezindie.com https://www.ezindie.com/feed/rss.xml晚晴幽草轩 https://www.jeffjade.com/atom.xml刘未鹏 Mind Hacks http://mindhacks.cn/feed/IT 之家 https://www.ithome.com/rss/IT 之家 - 24 小时最热 https://rsshub.app/ithome/ranking/24hDecohack https://www.decohack.com/feedV2EX http://www.v2ex.com/index.xml月光博客 http://www.williamlong.info/rss.xmlZAKER 精读新闻 https://rsshub.app/zaker/focusread透明创业实验 https://blog.t9t.io/atom.xml36 氪 https://www.36kr.com/feed小众软件 http://feeds.appinn.com/appinns卡瓦邦噶！ » Feed https://www.kawabangga.com/feed离别歌 https://www.leavesongs.com/feed/风雪之隅 http://www.laruence.com/feed理想生活实验室 https://www.toodaylab.com/feed木遥的窗子 http://blog.farmostwood.net/feedMac 玩儿法 http://www.waerfa.com/feed掘金专栏 - 飞猪前端团队 https://rsshub.app/juejin/posts/3051900006845944有赞技术团队 https://tech.youzan.com/rss/iDaily 每日环球视野 https://plink.anyfeeder.com/idaily/today资源分享 - Telegram Channel https://rsshub.app/telegram/channel/res_share
-
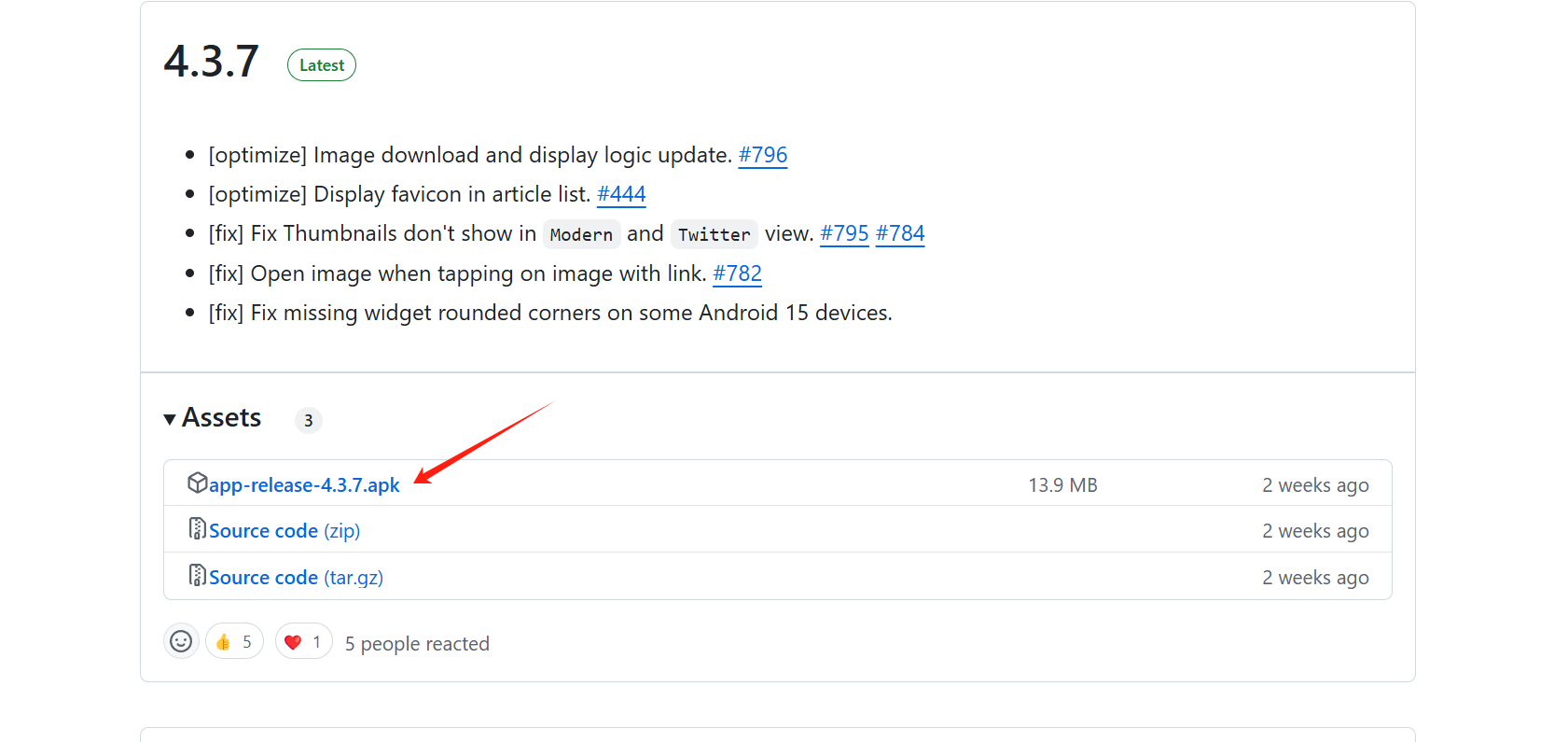
如何导入RSS订阅-附带软件下载地址 随着信息的大爆炸，越来越多的信息充满了我们的大脑，那么有没有一种节约手机内存还可以随时获取信息的办法呢？包有的包有的。这个叫做RSS，这玩意起源很早，曾经也是非常爆火的一个方式。说的直接一点就是信息聚合平台，那么我们应该如何获取呢？首先我们在GITHUB上面获取软件下载 下载地址 博主下载的时候版本是4.3.7版本，后续可能会更新，导入内容都大差不差的样子为什么推荐这个软件呢？原因很简单，这个软件自带魔法。导入之后不需要有其他的操作。关键是免费！免费！免费！接下来安装什么的我就不交了。直接导入，我这里用腾讯模拟器去弄首先点开软件，然后打开 如果没找到我直接把我网站的RSS地址放过来 RSS订阅地址 直接打开复制好，然后点击导入 导入RSS 然后就可以发现可以正常获取订阅源了，后续我也会更新一些比较好的订阅最后的效果图 欢迎订阅海绵博客！
-
深度解析蒸馏模型：与普通 LLM 的区别及低成本优势 在人工智能飞速发展的当下，大语言模型（LLM）和蒸馏模型成为了人们热议的焦点。它们在自然语言处理领域发挥着重要作用，但又有着各自独特的特点。今天，就让我们一起来深入探讨一下什么是蒸馏模型，它和普通的 LLM 有何区别，以及为何它的成本会如此之低。一、什么是蒸馏模型蒸馏模型，其核心技术是模型蒸馏（Knowledge Distillation，KD） ，简单来说，这是一种知识迁移技术，目的是将复杂且性能强大的教师模型（通常是大模型）所蕴含的知识，传递给相对简单、规模较小的学生模型。我们可以把教师模型想象成一位知识渊博的大学教授，他虽然拥有深厚的知识储备和强大的能力，但是在实际应用中，就像一位体型庞大的巨人，计算量巨大、运行速度较慢，并且需要大量的资源支持，比如强大的硬件设备和高额的能耗成本。而学生模型则像是教授的得力助教，经过知识的提炼和精简，虽然参数量较少，但仍然保留了大部分关键知识，并且能够快速高效地运行，对硬件资源的需求也相对较低。以大家熟悉的教学场景来类比，在传统的学习过程中，学生们往往是通过记忆标准答案（硬标签）来学习知识，就像普通模型在训练时只是简单地学习数据的标签。而在模型蒸馏的过程中，学生模型学习的是教师模型的解题思路和思考方式，也就是 “软标签”。例如，对于问题 “2+2 等于几”，教师模型给出的答案可能不仅仅是 “4”，还会给出每个答案的概率分布，如 {'4': 0.8, '3': 0.1, '5': 0.1}，这种软标签能够让学生模型学到更多关于答案可信度的信息，从而更好地理解知识，提升泛化能力。具体实现模型蒸馏，一般需要经过以下几个步骤：首先，训练一个性能强大的大模型作为教师模型，例如 GPT-4、DeepSeekR1 671B 这样的超大规模模型；然后，使用这个教师模型对数据进行推理，生成包含丰富信息的软标签；最后，利用这些软标签来训练小模型（学生模型），让学生模型学习教师模型的决策方式，从而具备接近大模型的能力。二、蒸馏模型与普通 LLM 的区别模型规模与结构普通的 LLM 通常具有庞大的参数规模和复杂的模型结构，以 GPT-4 为例，其拥有数以万亿计的参数，模型结构设计也极为复杂，旨在通过大规模的数据训练学习到丰富的语言知识和语义理解能力。而蒸馏模型则是从大模型中提炼知识，参数规模大幅减少，模型结构也相对简化。例如，基于 GPT-4 蒸馏得到的小模型，其参数可能只有原模型的几分之一甚至几十分之一，结构也更加紧凑，这使得蒸馏模型在运行时所需的计算资源和存储资源大大降低。计算资源需求由于模型规模和结构的差异，两者在计算资源需求上有着显著的不同。普通 LLM 在训练和推理过程中需要消耗大量的计算资源，需要使用高端的 GPU 集群，如 GPT-4 在训练时可能需要数千个甚至上万个顶级 GPU 协同工作，并且需要持续运行很长时间，这不仅对硬件设备的性能要求极高，而且能耗成本巨大。相比之下，蒸馏模型因为参数少、结构简单，在训练和推理时对计算资源的需求大幅降低，可能只需要少量的普通 GPU 甚至在 CPU 上就可以运行，大大降低了计算成本和能耗。性能表现虽然蒸馏模型在参数规模和计算资源需求上远远小于普通 LLM，但在性能表现上，它并非完全处于劣势。通过巧妙的知识蒸馏技术，蒸馏模型能够保留大模型的大部分核心能力，在一些特定的任务和应用场景中，其性能表现甚至可以接近大模型。例如，在某些对语言理解和生成要求不是特别高的场景下，蒸馏模型能够快速地给出准确的回答，并且在处理速度上比普通 LLM 更具优势。不过，需要注意的是，在面对复杂的、需要深度语义理解和强大推理能力的任务时，普通 LLM 凭借其庞大的知识储备和复杂的模型结构，仍然具有明显的优势。应用场景普通 LLM 由于其强大的语言理解和生成能力，适用于对语言处理能力要求极高的场景，如复杂的文本创作、智能客服中的复杂问题解答、高精度的机器翻译等。而蒸馏模型则凭借其轻量级、低成本、高速度的特点，更适合应用在资源受限的设备和场景中，如手机端的语音助手、智能手表的交互应用、边缘计算设备上的简单语言处理任务等。此外，蒸馏模型还可以用于对大模型进行快速的预评估和验证，在一些对实时性要求较高的在线服务中，也能够发挥重要作用，降低 API 调用成本。三、蒸馏模型成本低的原因硬件成本降低如前文所述，蒸馏模型的参数规模小，模型结构简单，这使得它在训练和推理过程中对硬件设备的要求大幅降低。不需要使用昂贵的高端 GPU 集群，普通的 GPU 甚至 CPU 就能够满足其运行需求。例如，一些基于蒸馏技术的小型语言模型，在普通的家用电脑上就可以进行推理运算，这大大降低了硬件购置成本和维护成本。而且，由于对硬件性能要求不高，设备的能耗也相应减少，进一步降低了运营成本。数据标注成本减少在模型训练过程中，数据标注是一项耗时费力且成本高昂的工作。而蒸馏模型可以利用教师模型为无标签数据生成 “伪标签”，这些伪标签可以作为训练数据，从而避免了大量的人工标注工作。在大规模无标签数据场景中，这一优势尤为明显。此外，教师模型还可以对原始数据进行优化，生成更适合小模型学习的数据分布，提高数据利用率，减少无效训练，进一步降低了数据相关的成本。训练时间缩短蒸馏模型的训练过程相对简单，因为它不需要像普通 LLM 那样在大规模的数据上进行长时间的复杂训练。它主要是学习教师模型已经提炼好的知识，所以训练时间大大缩短。例如，一些大型的普通 LLM 可能需要数月的时间进行训练，而基于其蒸馏得到的小模型可能只需要几天甚至几个小时就可以完成训练。训练时间的缩短不仅意味着可以更快地将模型应用到实际场景中，还减少了计算资源在训练过程中的持续消耗，降低了时间成本和能耗成本。模型维护成本低蒸馏模型的结构相对简单，这使得它在维护方面更加容易。不需要专业的大型运维团队和复杂的维护流程，普通的技术人员就可以对其进行日常维护和管理。而且，由于模型的更新迭代相对较快，蒸馏模型可以更灵活地适应不同的应用场景和需求变化，在模型更新时也不需要投入大量的人力和物力资源，降低了长期的维护成本。综上所述，蒸馏模型作为一种创新的技术，通过巧妙的知识迁移和模型优化，在与普通 LLM 有着明显区别的同时，展现出了显著的低成本优势。它的出现，为人工智能在更多领域的广泛应用提供了可能，尤其是在资源受限的场景中，蒸馏模型将发挥越来越重要的作用。相信随着技术的不断发展和完善，蒸馏模型将在未来的人工智能领域绽放出更加耀眼的光芒。
